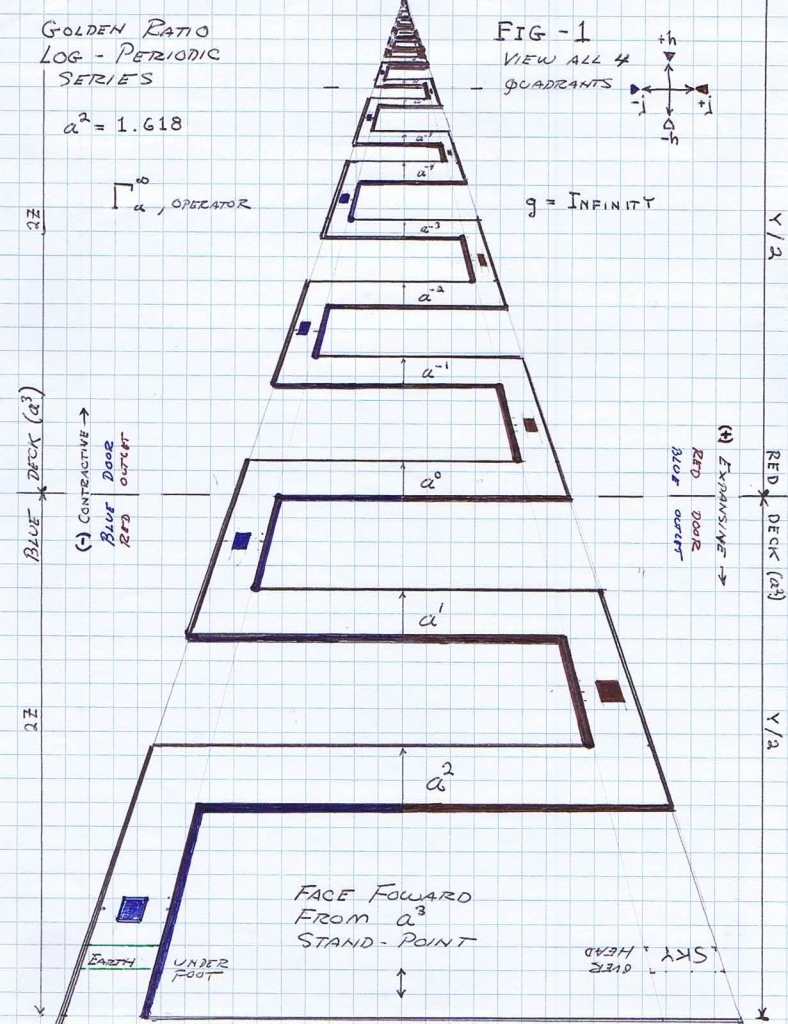
(1) In the previous series of writings on the “Bolinas Antenna” a rudimentary log-periodic operator was developed,
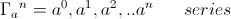
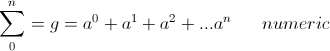
This operator is a span of logarithmic periods. The span is a finite section taken from an infinite log-periodic series of log-cycles. To the right of the span is an infinite progression growing larger and larger, to the left of the span is an infinite regression shrinking smaller and smaller. The arch-form of the log-periodic series is the broadside log-periodic array developed in the previous writings on the Bolinas Antenna, it can be seen looking at this structure the appearance of expression for infinity.
This is an intrinsic characteristic of a log-periodic geometry. The log-periodic sequence is a scaling factor of proportionality and serves as an innate property of human perception, hence the “Deci-Bell”.
(2) The human scale factor in the dimensions of sound is a span from 32 ft to 3 inches as expressed by the pipe organ. This span represents the sequence of human versor positions in the infinite log-periodic sequence of the musical universe. This relates directly to the original Pythagorean concept of music, the expression of man’s POSITION in the cosmos.
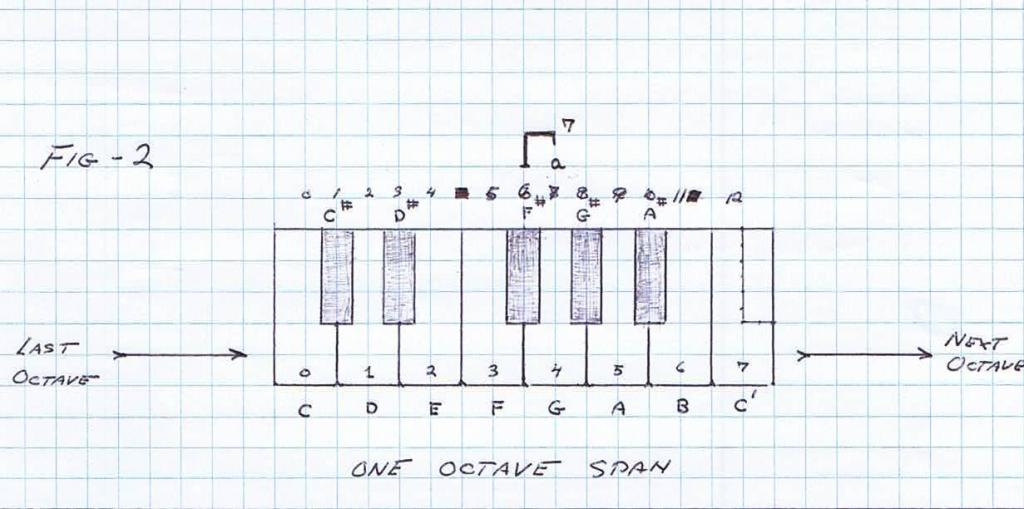
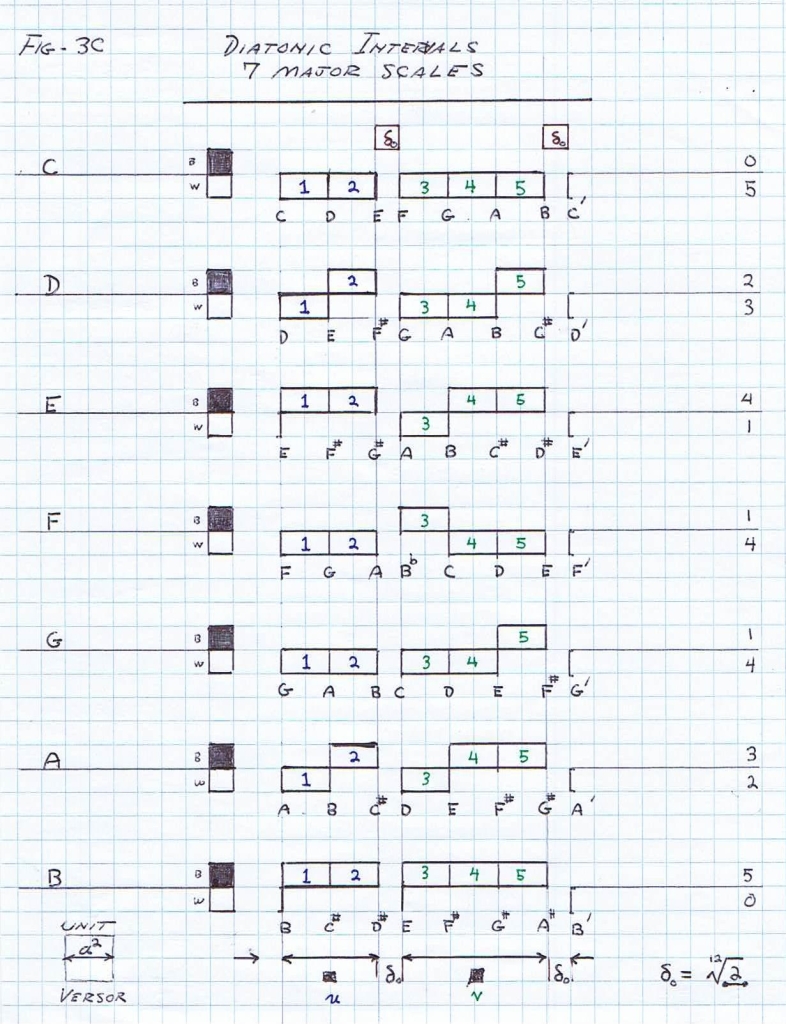
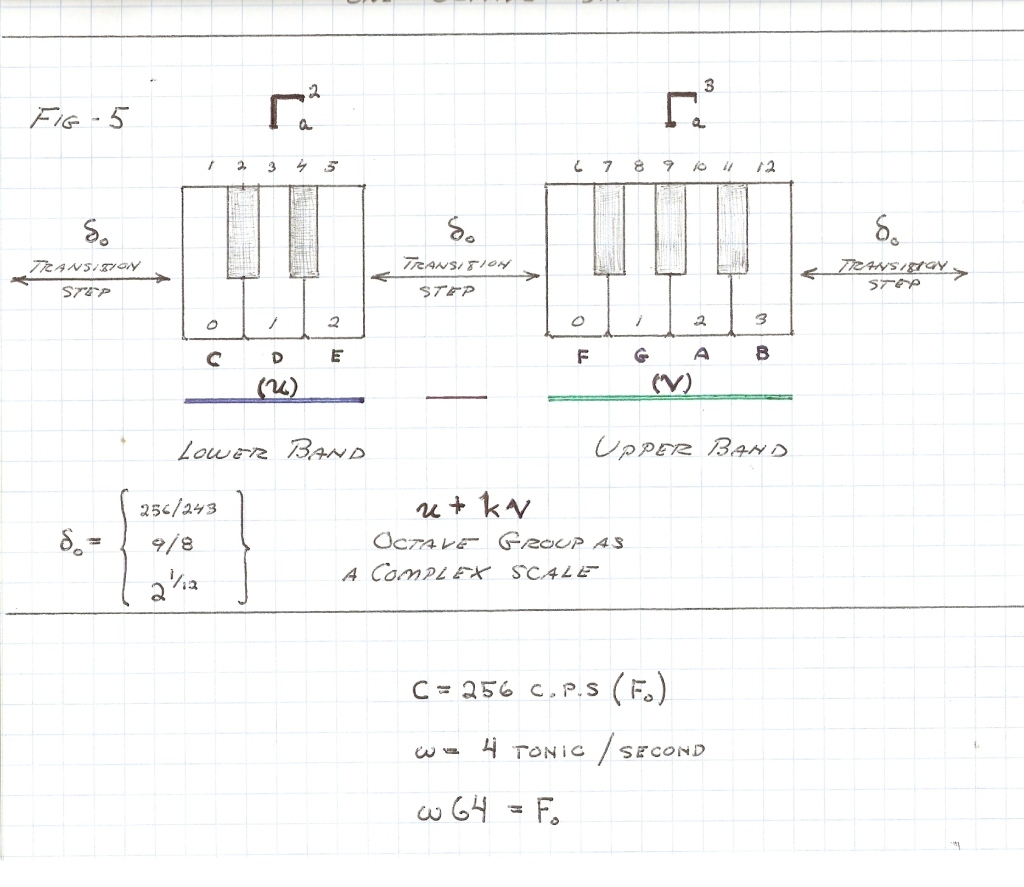
(3) The span of keys on the standard music keyboard is a log-periodic sequence. There are 88 individual keys or “notes” these representing unit versor positions of the various musical scales. Each fundamental span from the Tonic C to the Octave C, is a single log-periodic cycle called the octave cycles on the standard music keyboard.
The entire span of human hearing is about 10 octave cycles. Each cycle, or period, on the music keyboard is divided into 12 subdivisions, that is 12 keys constitute one octave, Fig 2.
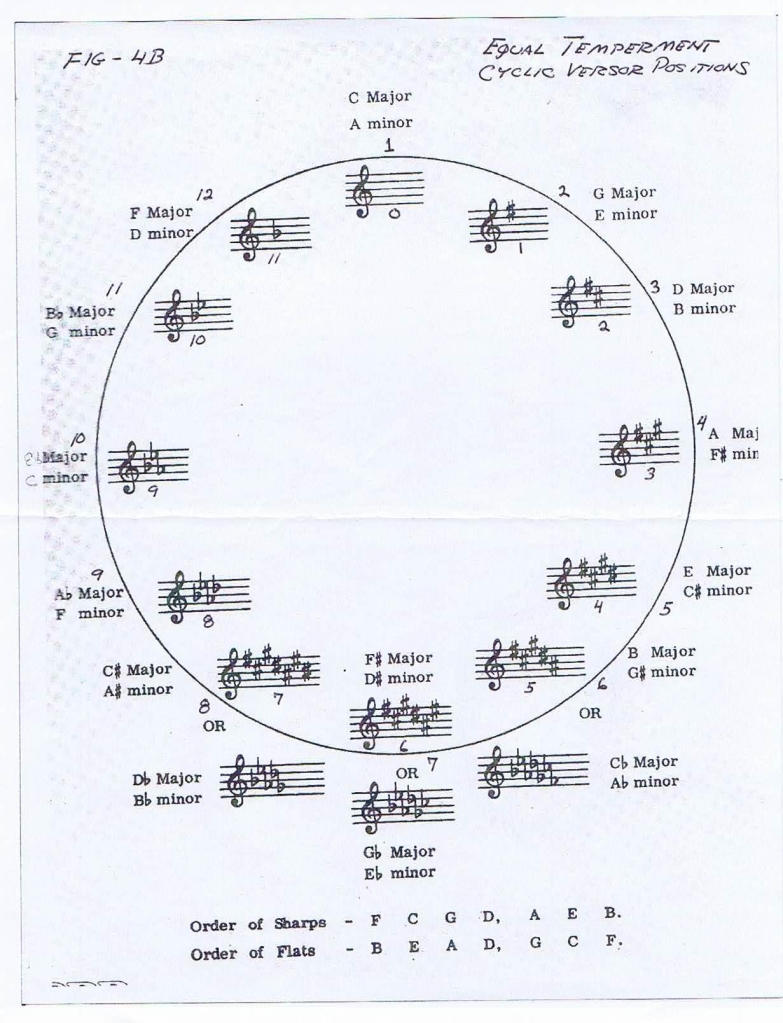
A variety of versor systems derive from this octave span of twelve unit divisions. In symbolic form the octave is given by
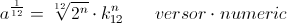
where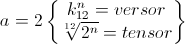 
For the fundamental scale of the Pythagorean Lydian mode or C major diatonic mode,
n = C, D, E, F, G, A, B
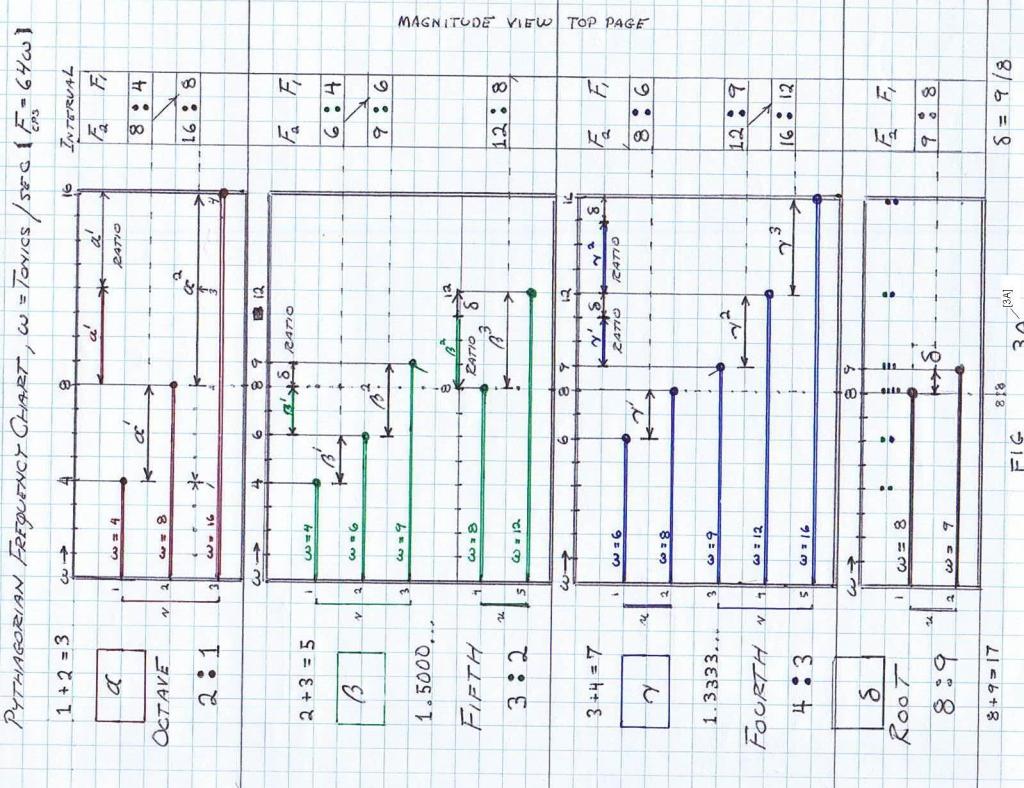
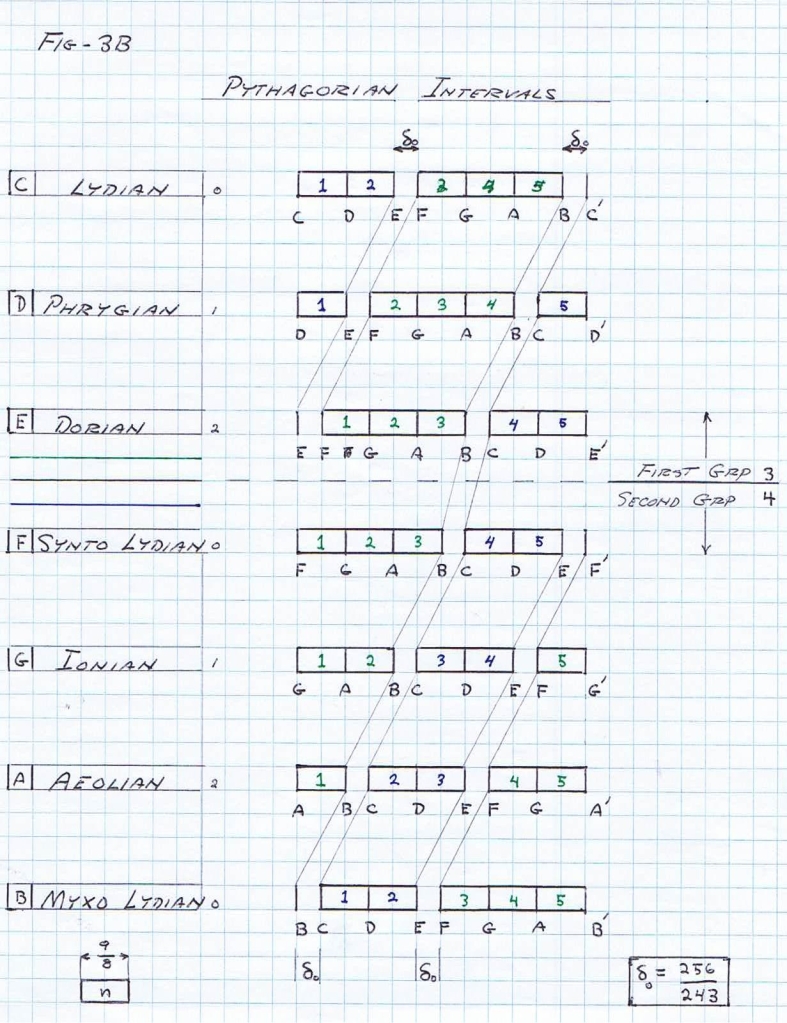
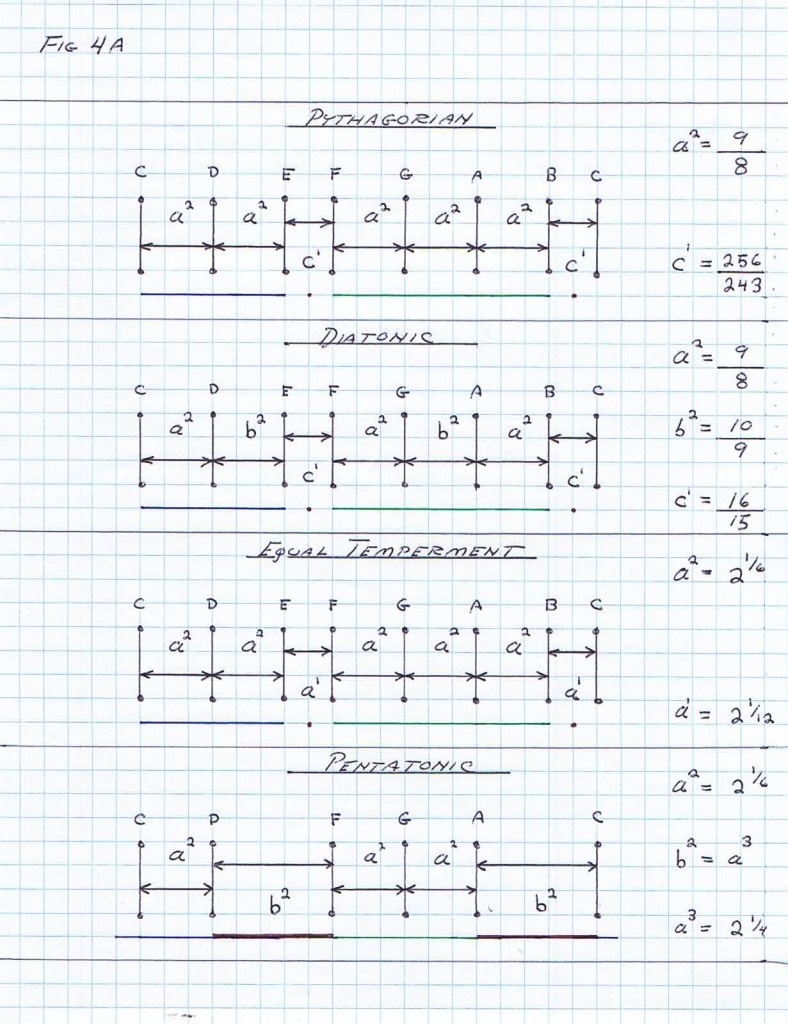
each versor system or music scale is a division of 7 keys or unit versor positions, Figs 3 & 4.
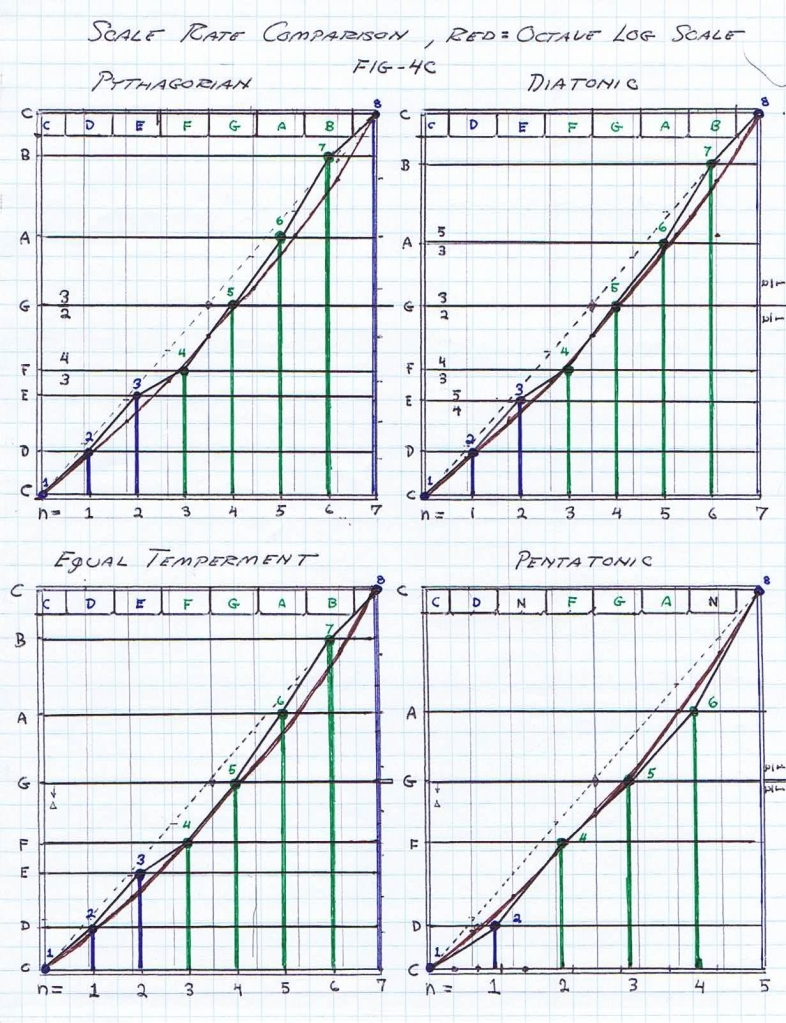
(4) This symbolic representation by versor operators is of a most complex form. The first complications is that the unit versor positions are not distributed in a uniform fashion, Fig 4C.
Neither linear, nor logarithmic, and exist in an uneven connection of sub-versors, Fig 5.
Another complication is that a pair of dimensions exist rather than only one. Here exists both the dimension of space as a wavelength, and the dimension of time as a pitch. The product of this pair of dimensions, length and one over Time, is the dimensional relation for velocity, a constant. Hence a velocity versor, and a similar relation to the light-second of Steinmetz. The product of two terms equal to a constant is a hyperbolic function, zero pitch – infinite wavelength, and zero wavelength – infinite pitch. This relation is shown by the logarithmic curve that is characteristic of a rank of organ pipes.
Moreover another complexity is a third dimension, that of the human mind. The mind regards the log-periodic span of one octave as once complete cycle, a circular function, whereas the log-periodic cycle is a hyperbolic function. Hereby the complete symbolic, or versor, operator for musical expression has a complex interrelation in three distinct dimensions
(I) Mind (Melody)
(II) Time
} (Velocity)
(III) Space
Because of this complex situation the symbolic operator for music has never been fully resolved. What has developed is a distributed correction factor resulting in the musical intervals becoming a bit out of tune. A complete Pythagorean cycle of unit versor positions results in the terminal pitch being a bit high in frequency. This represents a distortion factor known as the “Pythagorean Comma”,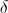 
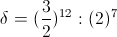
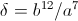
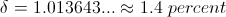
(5) The various geometric forms established by log-periodic networks, transient or oscillatory electric waves, and musical scales, engender the concept of a hyperbolic versor operator. The primordial elements of this operator are to be found in the writings of ; Dr. Alexander Macfarlane, University of Austin, Texas;
And of Arthur Kennelly, Edison General Electric.
The symbolic operators of antiquity serve as templates of a hyperbolic versor operator, and hence enter the subject.
The hyperbolic versor operator exists in contra-distinction to the circular versor operator. The familiar circular versor operator was employed by Steinmetz but the hyperbolic versor remains an enigma. Steinmetz rejected the hyperbolic versor, but then Pupin rejected Steinmetz’s circular operator, the usual sequence of rejection, ask Oliver.
(6) The circular operator is expressed in one of two forms;
Cycles per Second, F,
or Radians per Second,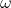 
And the hyperbolic operator is expressed in one of two forms;
Decibels per Second, dB,
or Nepers per Second, u.
Radians and Nepers are the proper expressions for use as exponents of the natural log based epsilon, 
Epsilon is defined by the relations
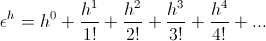
where
.
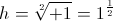This infinite series gives a pair of numerical values for Epsilon,
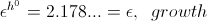
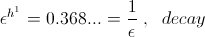
(7) In contemporary engineering mathematics the circular and hyperbolic functions are derived by means of the natural log base. The circular functions are derived from the infinite series as powers of the square root of negative one
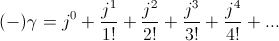
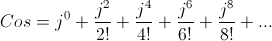
The hyperbolic functions are derived from the infinite series as powers of the square root of positive one,
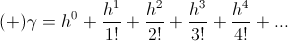
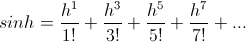
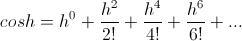
The functions of the natural log base, , introduces the limitation that operation is only possible in Cartesian relations, that is, a system of rectangular co-ordinates or the octaves thereof. This log-base and its related functions, sin, cos, etc. are incapable of expressing numerical versor divisions not derived from the log-periodic series of the octave,
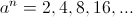
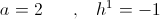
and it’s versor operators,
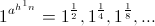
Therefore a division of three units such as encountered in three phase electrical systems cannot be expressed as exponents or functions of the natural log base, . The poly phase operator must first be reduced to its Cartesian equivalents. The three phase operator is given symbolically as
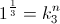
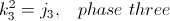
In Cartesian equivalents it is
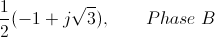
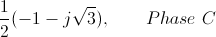
where j is the Steinmetz quadrantal operator.
(8) Expressions for the depth of penetration of electro-magnetic induction into metallic substances involve an octic (8) versor relation. This gives rise to a pair of somewhat incongruous results. From the versor expression
is derived the unit octic (8) versor of the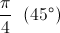 
lag in metallic back E.M.F.
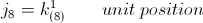
However in vector Cartesian form the symbolic expression for an octic is,
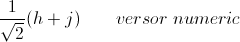
where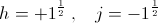 
and the derived unit octic lag of 45 degrees is given by
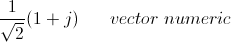
where j is the steinmetz quadrantal operator.
Here evoked is the idea of Oliver Heaviside that the vector and the versor should not be intertwined. The octic versor is developed in the “Generalized Electric Wave” by E.P. Dollard.
(9) Steinmetz ardently opposed higher order versors and reduced everything to Cartesian form. To Steinmetz the quadrantal versor of Cartesian expression “therewith closes the field of algebra”. “Thus within the range of algebra no further extension of the system of numbers is necessary or possible, and the most general number is
a + jb.”
The engineering form of the versor operator was born by Steinmetz but was killed at birth, frozen into vector Cartesian form.
(10) Polyphase versor operators however continued to develop into a symbolic form known as “symmetrical components”, and related versor operators have come to be called “sequence operators”. This symbolic representation is a natural extension of the Steinmetz “Roots of the Unit” in “Theory and Calculation of A.C. Phenomena”. This also is reduced to Cartesian expressions but is worthy of further study with the objective of developing polyphase versor operators. The system of symmetrical components originated in a paper before the American Institute of Electrical Engineers by Charles Fortecuse. This paper was published in the transactions of the A.I.E.E. Volume 37, 1918, page 1027. The title is, “Method of Symmetrical Coordinates Applied to the Solution of Polyphase Networks”. A later article is presented by C.F. Wagner and R.D. Evans in the “Electrical Journal”, April, 1928, page 194, titled, “Symmetrical Components”. This evolved into a book by Wagner with the same title as the article. More will be written on this later.
(11) The versor operator is born of mathematical impossibilities. This can be noticed in historical references discussed by A. Macfarlane in his papers. This evokes the often stressed statement by Oliver Heaviside that “mathematics is an experimental science,” it certainly was in the time of antiquity. The quadrantal versor operator employed in the Steinmetz method is derived from a mathematical impossibility, the square root of a negative number. The “Roots of the Unit” give rise to versor operators derived from a meaningless mathematical statement, a base one log system. Moreover the log-periodic operator in its entirety is numerically equal to infinity. It is hereby evident that the generalized symbolic versor operator, the principle objective in this series of writings, will not be born of accepted notions of mathematics. This operator is of a strange world, such as expressed by Lewis Carrol’s “Thru the Looking Glass”. This looking glass is Johannas Kepler (1571-1630) and on the back side is the world of mathematics that preceded him. It is a return to the very origin of numbers, mathematics, and the inscrutability of the ideas of Nikola Tesla. This path leads directly back to Pythagoras of Samos.
(12) Aristotle (384 BC – 322 BC) gives an account of the Pythagorean philosophy in his book “Meta Physics”. Here Aristotle makes the following statements:
(I) “The Pythagoreans, as they are called, devoted themselves to mathematics;”
(II) “They were the first to advance this study, and having been brought up on it they thought its priciples were principles of all things”.
(III) “Since the principles of numbers by nature are the first, and in numbers they seemed to see many resemblances to things that exist or come into being”;
(IV) “Since again, they say that the attributes and ratios (Logos) of the musical scales were were expressible in numbers, since again, the Pythagoreans say that the attributes and ratios of the musical scale were expressible in numbers”;
(V) “Since, then, all other things seemed in their whole nature to be modeled after numbers, and numbers seemed to be the first things in the whole of nature, they suppose the elements of numbers to be the elements of all things and the whole heaven to be a musical scale and a number.”
Here is an expression of a generalized symbolic operator. This concept led to a symbolic operator developed by Robert Fludd (1574 – 1637 AD), it is known as the “Divine Monochord”.
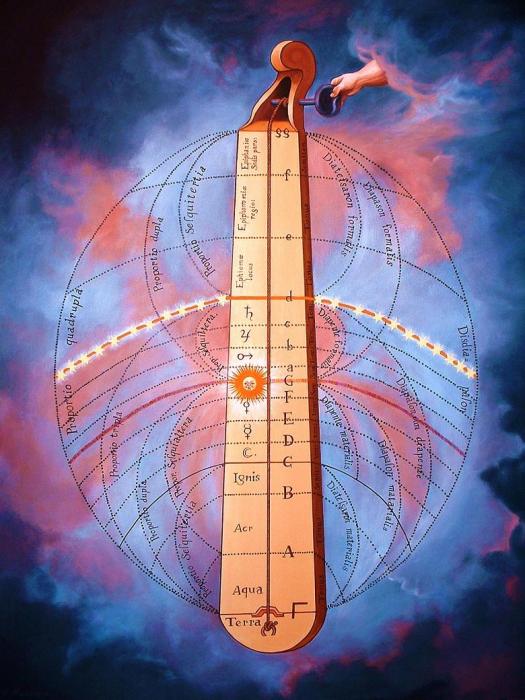
This “instrument” serves as a versor analog computer for the Solar System, and in a strange way also for the Tesla Magnifying Transciever. It represents a musical hyperbolic versor operator. Beginning with the Earth at gamma,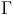 
, GROUND, the Monochord progresses thru the four elementals, the Sun, Moon, and the known planets, and moreover thru the unknown planets, terminating on g, the planet Pluto. At the tip of the Monochord the hand of God, AERIAL, sets the cosmic constant (a.k.a. one over c square) and thereby sets the cosmic pitch of the Divine Monochord. What is important to notice here is that not only did Uranus, Neptune, and Pluto evade notice in this era, but their very existence would have been decried a disruption in the “Universal Order” that had already become an institution. Yet these three unknown planets are implicit in the Divine Monochord.
(13) The Pythagorean point of view is that numbers are like operators, expressed as (music) ratios (logos), or in pure symbolic forms.
Their use for counting is a secondary consideration. The present era use of numbers bears no resemblance to that of ancient times. Today it is numeration not numerology.
On a practical level this is why the ideas of Nikola Tesla are so incomprehensible to the modernistic way of thinking. It is a given in the “Mind of Today” that Tesla was a “little funny in the head”, this in part because of his manner of co-ordinating his lifes movements with numbers divisible by three. His “refugee room” number during his tacit exile was 3327. It is very important to consider that this threedom would not sound at all strange, not in the least, to Johannas Kepler. Entire chapters on the power of the number three were written prior to Kepler’s time. Moreover Nikola Tesla received his education in the classics at Graz, the very location in which Kepler taught geometry centuries before. Here is where Kepler discovered the mathematics of the Solar System. This explains how Nikola Tesla developed his incredible creative power. Tesla gained the ability in his mind to transform directly from the cosmic level to the Earth level from 
, resulting in a physical manifestation, the working apparatus. His ability to carry out his objectives is derived from the hermetic traditions of Ancient Aegypt, not from pendantic technical training. It can be said that the inability of the modernist to understand Tesla is not because of technical complexity but because of Divine Simplicity. Moreover the modernist has a deep seated pathological contempt for any pre-Kepler concept of a harmonic universe particularly when expressed in a numerological form. This odious animosity for Tesla’s methodology is of such force that even the military and industrial organizations are denied the work of Nikola Tesla. See Vassilatos, “Secrets of Cold War Technology”, introductory chapters.
(14) In closing on the subject of the symbolic operators of antiquity is an ancient era equivalent to today’s “Theory of Relativity”. In the universe of human cultures that inhabited this Earth thru the eras of ancient times it was generally considered that the Sun was the center of things, the major heavenly bodies rotated around it. It was considered a heliocentric universe. Great cultures grew upon this understanding. Then it came to pass in the second century A.D. Someone came up with the notion of geocentric relativity. This someone was Ptolemy (90 A.D. – 168 A.D.). His theory of relativity stated that all heavenly bodies now move relative to the Earth as the center, hence geocentric relativity. Geocentricity would poison astronomy for fourteen centuries following its inception. It became a plethora of correction factors, adjustments, and the like, rendering the advance of astronomy impossible. Geocentricity was a pioneering philosophy for the Dark Ages. Geocentric relativity was to become the law of the church with capital punishment. Bruno was burned at the stake for “practicing” heliocentricity and Galileo was exiled for finding that the planets indeed revolved around the Sun. The heliocentric philosophy of Copernicus was banned in this era with the same fervor that the philosophy of Tesla is banned today by the existential modernists. Upon the unification by Kepler of the geometric, heliocentric, and related Pythagorean concepts there could be no more opposition to a heliocentric Solar System of a unit form existing in the generalized heavens.
(15) Modern relativity and its autistic child quantum mechanics are historical analogs to the condition of Ptolemy and the institution that followed him. In modernistic relativity it is now that one over c square is the center of the universe with time and space revolving around it. The quagmire of correction factors and systems of distorted co-ordinates developed into a schizophrenic institution known as quantum mysticism. Even beyond geocentricity, this is verily a pathological anthropocentricity, a lemming march into the Kurtzwiel grand singularity of universal annihilation. It is to be made law.
73 DE N6KPH
Reference:
1) “Music of the Spheres” – Jamison
2) “Le Modular” – Corbisier
3) “Harmonograph; A Visual Guide to the Mathematics of Music” – Ashton, Wooden Press.