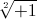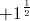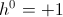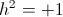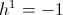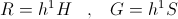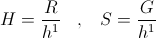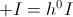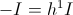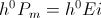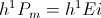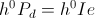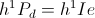Since Electrical Activity, or Power, P, in watts, is the product of this Constant Potential, e, and a Displacement Current, I, which is zero, the Activity, or Power is also zero. Thus in the absence of Displacement no power is required to maintain a static Dielectric Field of Induction, Fig 1B.
A violent magnetic discharge, in the form of an intense forward E.M.F., results from the path for current, i, being broken, or open circuited. This forward E.M.F. is the result of the stored energy within the Magnetic Field acting to maintain a continuous current, and its M.M.F., which now has been disrupted by an open circuit. An open circuit is the denial of any current flow, thus an infinite E.M.F. is developed within the Metallic-Dielectric Geometry of the Inductance. Fig 1C.
Likewise, a violent dielectric discharge, in the form of an intense Forward Displacement Current, results from the Potential, e, being Short Circuited. This Forward Displacement is the result of stored energy within the Dielectric Field acting to maintain a Continuous Potential which now has been disrupted by a short circuit. A short circuit is the denial of any Potential, thus an infinite Displacement is developed within the metallic-dielectric geometry of the Capacitance. Fig 1D.
The Flow of Power, or Activity, is indefinite in all four of the above conditions. No products can be formed since it is either the current is zero, or the potential is zero. The energy involved is only that contained in the Fields of Induction themselves, no energy exchanged, or transfer, exists with outside forces. The static charge, or Transient Discharge must remain within the metallic-dielectric geometry of the Inductance, or the Capacitance.
For the static case, the energy remains in a signal form, magnetic or dielectric. For the disrupted case, the energy escapes into its conjugate form within the Counter-Spatial Dimensions of the Inductor, or the Condenser, containing the energy involved. For the Disrupted Magnetic Discharge the extreme E.M.F., E, becomes an extreme electro-static potential, e, thus the energy escapes into Dielectric Form within the Inductor.
Likewise, for the disrupted Dielectric Discharge, the extreme displacement, I, becomes an extreme M.M.F., i, thus the energy escapes into Magnetic Form within the Condenser. Because no energy is dissipated, powerful electric oscillations are produced within the Inductor or Condenser. The trapped energy is continuously reflected to and fro between Magnetic & Dielectric Forms within the metallic-dielectric geometry of the device. Little Theoretical or Experimental knowledge exists on this subject, but here enters the work of Nikola Tesla, and his disruptive discharge apparatus.
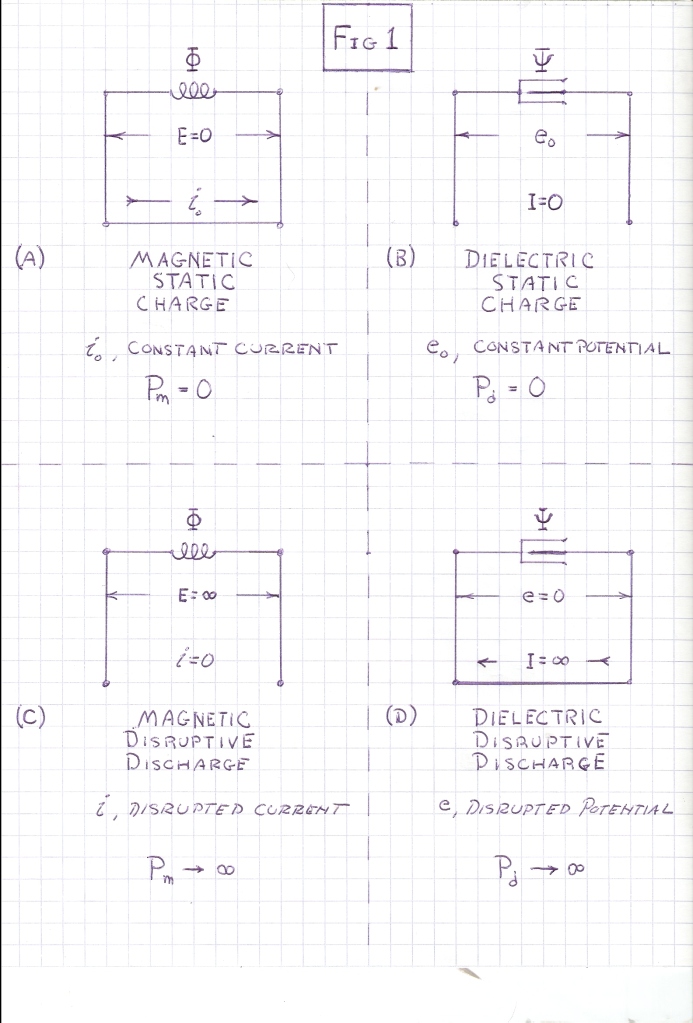
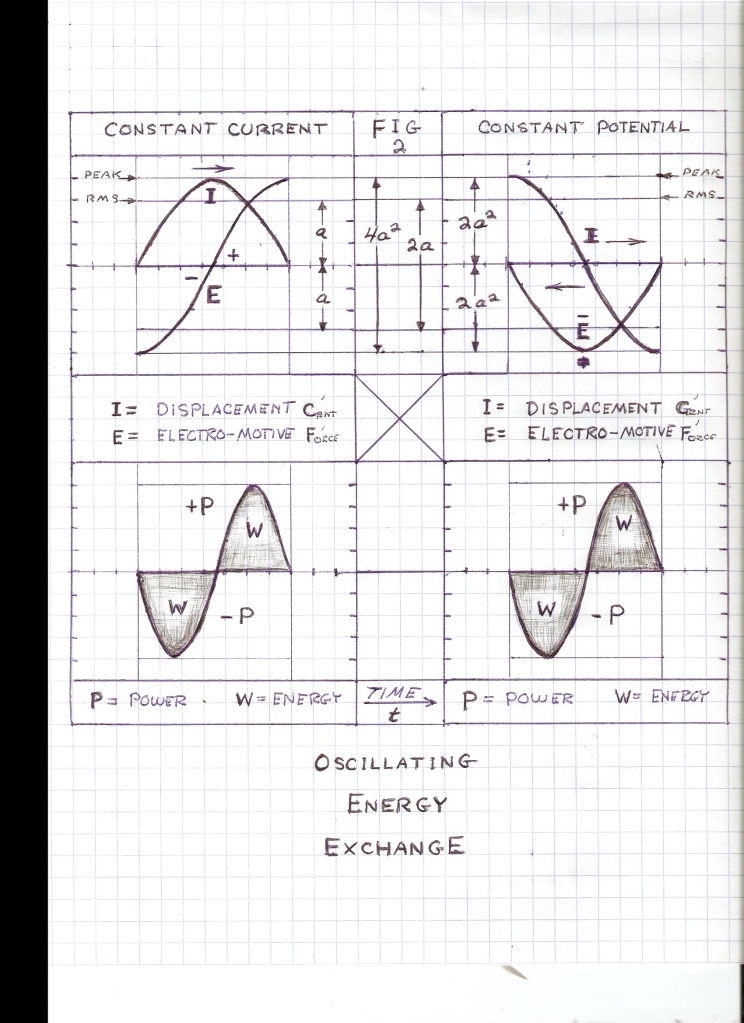
When the energy contained within the Fields of Induction is delivered to, or taken from, external forms, a set of relations exist as shown in Fig 2. This condition of energy transfer involves Electrical Activity, or Power, P, in watts. Power is The Time Rate of Energy Transfer into, or out of The Field of Induction. The Dimension of Time now takes part. Thus energy transfer gives rise to Frequencies and Time Constants.
For this condition of External Energy Transfer, the external device is a specifically constructed drycell, this the size and shape of the common “D” cell as used in a flashlight. This drycell has virtually no internal losses. It also has been proportioned to have a Natural Impedance of one ohm, and thus a Natural Admittance of one siemens. Hence the following characteristics of this “XD” drycell;
Open Circuit Potential, eo, 1 Volt
Short Circuit Current, io, 1 Ampere
And thus the ratio of one volt to one ampere is
Natural Impedance, Zo, 1 Ohm
The Polarity markings for eo and io are shown on the drycell in Fig 2.
This unit drycell is hereby a source of Constant Potential to a Charged Condenser of Equal Potential, and a source of Constant Current to a Charged Inductor of the Same Current. The Displacement or E.M.F. is zero. In both conditions the energy is static, no Transfer of Energy takes place giving rise to Activity. The Power is zero thus the conditions revert to those of Fig 1A & 1B.
This unit drycell contains a certain quantity of Stored Chemical Energy. This Chemical Energy can be taken out and delivered to an external form, or it can be given back to Chemical Form within the drycell, taking energy from an external form. Energy can be taken from or given to this unit drycell, it is rechargeable.
This unit drycell thus can be a Negative Resistance, or a Negative Conductance, when supplying Energy to External Forms. It also can be a Positive Resistance, or a Positive Conductance, when taking energy from external forms. For the condition of constant current this unit drycell is a Positive Resistance, R, in ohm when taking in energy from an External Form, or it is a Negative Resistance, a “Receptance”, H, in ohm when giving out Energy to an External Form.
Likewise, for the Condition of Constant Potential this unit drycell is a positive Conductance, G, in siemens when taking in energy from External Forms, or a negative Conductance, and Acceptance, S, in siemens when giving out energy to External Forms.
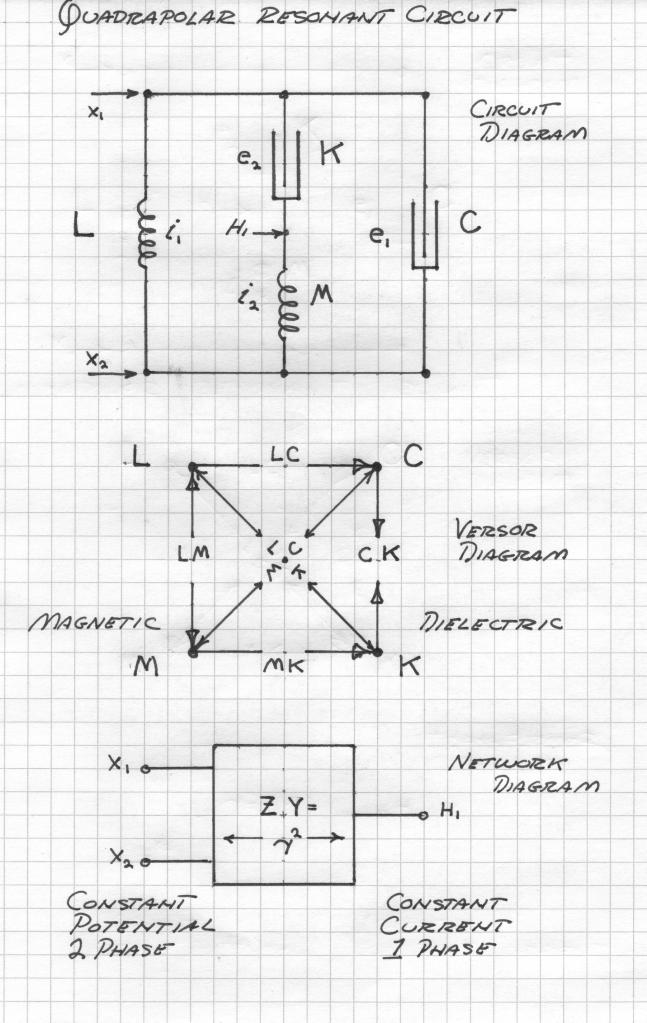
This unit drycell is here shown to be a bi-directional resistance or conductance. In ordinary Resistances R or Leakages G energy flow is always a uni-directional flow, out, in the form of Heat Energy commonly. Here then is a Versor Resistance, or a Versor Conductance. The D.C. Versor operator is derived from the expression,
(1)
Symbolically it is
(2)
With roots, +1 and -1
The versor operator becomes, for this D.C. condition of bi-directional flow,
(3)
And
…etc
Hereby the versor relations of the bi-directional device, such as the unit drycell are given
(4)
 The energy stored within the Magnetic Field of Induction can be supplied to, or taken from the unit drycell. Likewise the energy stored within the Dielectric Field of Induction can be supplied to or taken from the unit drycell. Whereas the disruptive circuit condition completely open circuits the Inductance, or completely short circuits the Capacitance, here now the unit drycell is inserted in the place of the open circuit, or the short circuit. Circuit Continuity is hereby maintained by the drycell. Energy can now be transferred in a finite manner.
The energy stored within the Magnetic Field of Induction can be supplied to, or taken from the unit drycell. Likewise the energy stored within the Dielectric Field of Induction can be supplied to or taken from the unit drycell. Whereas the disruptive circuit condition completely open circuits the Inductance, or completely short circuits the Capacitance, here now the unit drycell is inserted in the place of the open circuit, or the short circuit. Circuit Continuity is hereby maintained by the drycell. Energy can now be transferred in a finite manner.(1) The Energy, W, in Joules, stored in the Magnetic Field, Phi, in Weber, is delivered by Electrical Activity, P, in Watts, Fig 2A, to the drycell
(2) The Energy, W, in Joules, stored in the Dielectric Field, Psi, in Coulomb, is delivered by Electrical Activity, P, in Watts, Fig 2B, to the drycell.
(3) The Energy, W, in Joules, stored in the Magnetic Field, Phi, in Weber is derived from the Electrical Activity, P, in Watts, Fig 2C, out of the Chemical Energy of the drycell.
(4) The Energy, W, in Joules, stored by the Dielectric Field, Psi, in Coulomb, is derived from the Electrical Activity, P, in Watts, Fig 2D, out of the drycell.
Hence Magnetic Power Flow in watts can transfer energy from the Magnetic Field, or to the Magnetic Field, this energy to, or from, the Chemical Energy of the drycell. The flow of power is two way, or bi-directional. It is a differential quantity.
Likewise hence, Dielectric Power Flow in watts can transfer energy from the Dielectric Field, or to the Magnetic Field, this Energy to, or from, the drycell. Again the Power Flow is bi-directional, a differential quantity.
The Magnetic Inductance develops an Electro-Motive Force, E, during the Time of Energy Transfer with the drycell. This E.M.F. acts in conjunction with, or in opposition to, the Continuity of Current (M.M.F.), i, this developing the Electrical Activity, Ei, in watts, of Energy Transfer. This Activity, or Power, Pm, is the time rate of Energy Transfer.
Likewise, the Dielectric Capacitance develops a Displacement Current, I, during the Time Interval of Energy Transfer with the drycell. This Displacement acts in conjunction with, or in opposition to, the Continuity of Potential, e, this developing the Electrical Activity, Ie, in watts, of Energy Transfer. This Activity, or Power, Pd, is the Time Rate of Energy Transfer.
It hereby can be seen that the dimension of Time plays an important role in this Energy Transfer. Electrical Activity is the time rate of Energy Transfer,
Watt, or Joule per Second. (5)
The longer, more prolonged, time rate of transfer, the less in magnitude is the Power Flow. Likewise, the shorter, more instantaneous, time rate of transfer, the greater in magnitude is the Power Flow. The Disruptive Discharge is a Limiting Condition, and as well is the Static Charge. In both cases the Flow of Power is zero. The Energy remains within the Inductor or the Condenser.
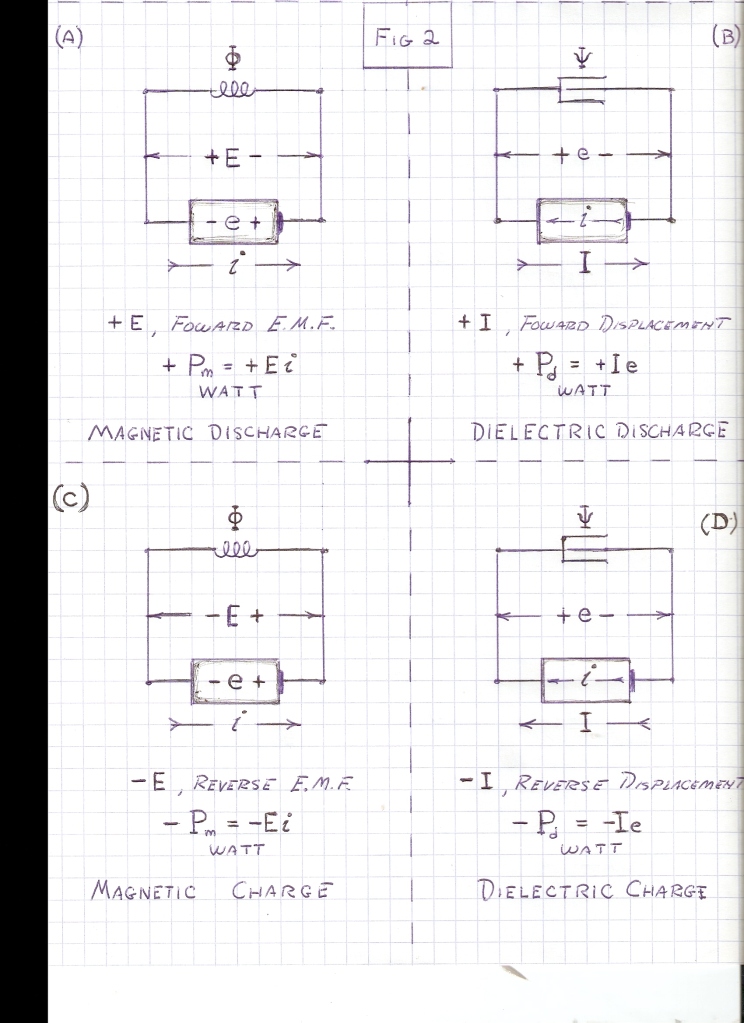
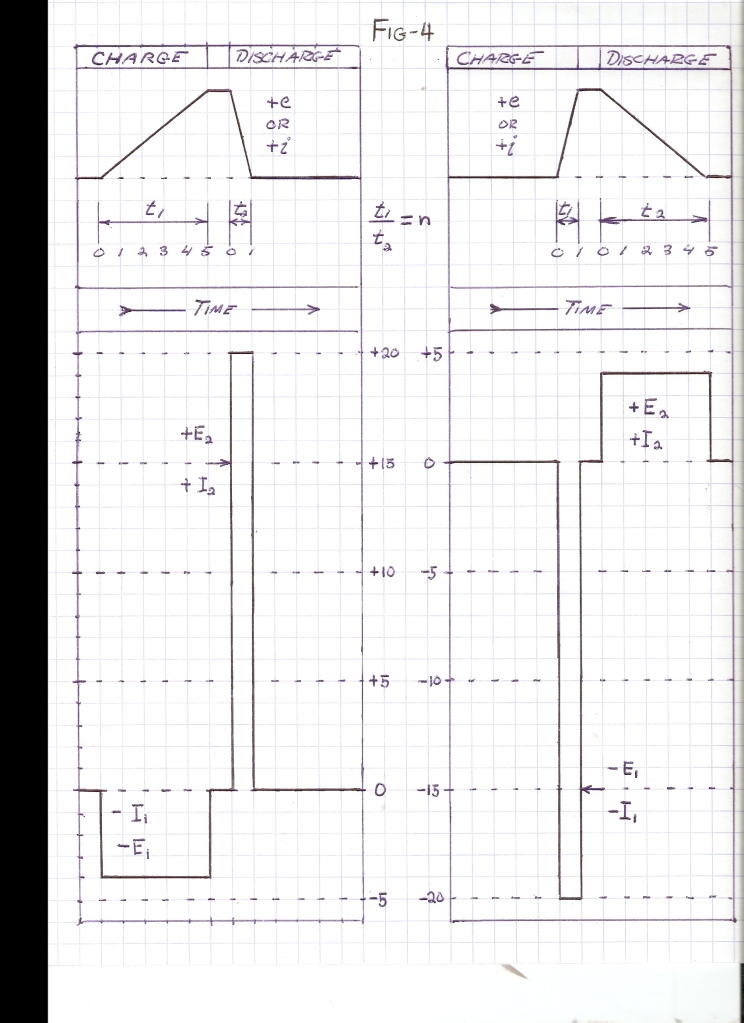
Thru adjustment of the time rate of charge, and the time rate of discharge, involved in Energy Transfer into, or out of, a Field of Induction, any magnitude of Electrical Activity, P, can be developed from a given quantity of stored Energy, W, Fig 3, Fig 4. Denoting the charge time as t1, and the discharge time as t2, taking the ratio as,
, Numeric (6)
The Power Magnification is given as
, Watts, (7)
And thru Energy Conservation, it is,
, Joules (8)
The factor n is called The Magnification Factor of Energy Exchange.
While a Magnetic Inductance is gathering energy from the Chemical Energy of the drycell, a backward directed E.M.F., E, is developed within this Inductance. This E.M.F. acts to maintain a constant M.M.F., or current, i, that is it acts to maintain the quantity of Energy Stored within the Magnetic Field. While an Inductance is delivering its Magnetic Energy to the Chemical Energy of The Drycell, a forward directed E.M.F., E, is developed within the Inductance. This E.M.F. also serves to maintain a constant M.M.F. or current, i, that is it acts to maintain The Quantity of Energy Stored within the Magnetic Field. Fig 2A & 2C.
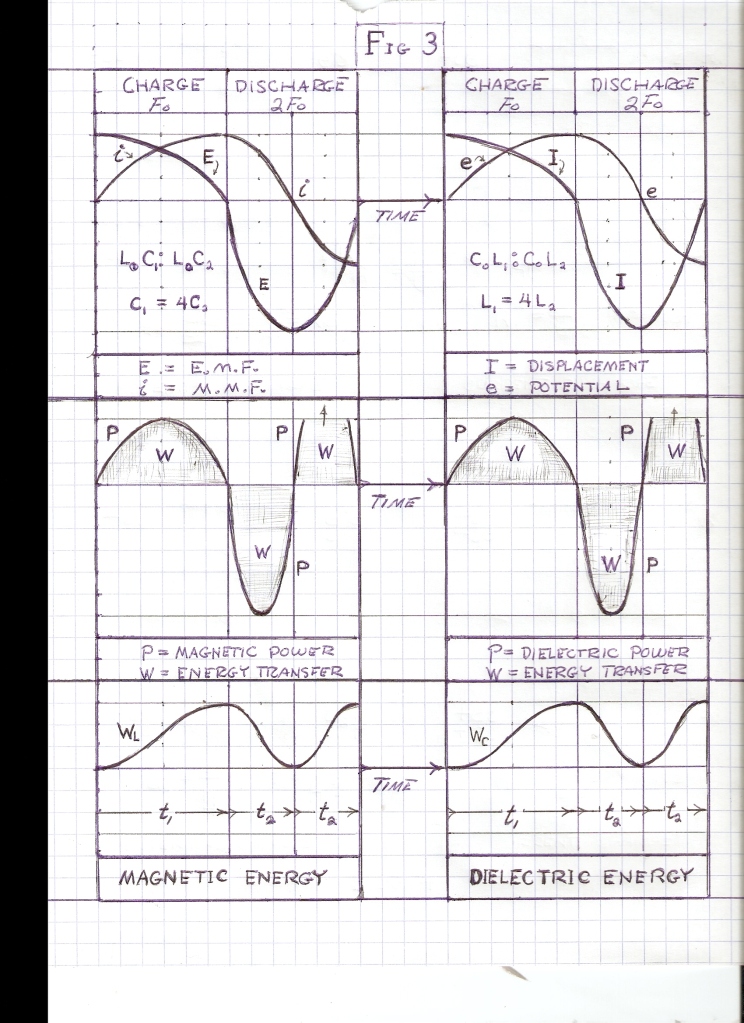
Hence the charging Inductance, gaining Magnetic Energy, develops an E.M.F., E, in opposition to the Potential, e, of the Drycell. The resulting Voltage Difference combines with the current, i, in delivering Energy to the Magnetic Field of Induction. This E.M.F. is called the “Back E.M.F.”. Also, the Discharging Inductance, losing Magnetic Energy, develops and E.M.F., E, in conjunction with the Potential, e, of the Drycell. The Resulting Voltage Summation combines with the current, i, in delivering Energy to the drycell. This E.M.F. is called the “Forward E.M.F.”. The E.M.F. is thus a differential magnitude, Back E.M.F. on charge, +E, Forward E.M.F. on discharge, -E. Fig 3.
Likewise, hence the Charging Capacitance ad Displacement Current, I, in opposition to the current, i, of the drycell. The resulting current flow combines with Potential, e, in Delivering Energy to the Dielectric Field, taking it from the Chemical Energy of the drycell. The Discharging Capacitance develops a Displacement Current, I, this in conjunction with the current, i, of the drycell, in Delivering Energy to the drycell, taking it from the Stored Energy of the Dielectric Field, Fig 2B & 2D. The Charging Displacement is called the “Back Displacement,” and The Discharging Displacement is called the “Forward Displacement”. Back Displacement, -I, Forward Displacement, +I, the displacement is a differential magnitude. Fig 3.
Hereby, The Four Primary Energy Transfer Relations
1) Magnetic Energy Discharge,
Forward E.M.F., Fig 2A.
2) Dielectric Energy Discharge
Forward Displacement, Fig 2B.
3) Magnetic Energy Charge,
Back E.M.F., Fig 2C.
4) Dielectric Energy Charge
Back Displacement, Fig 2D.
Note, the unfortunate condition exists that the Production of Energy is taken as a Negative Value, the Consumption of Energy is taken as a Positive Value. However, this is the established convention, despite the confusion it creates.
The following relations for power flow are hereby derived,
MAGNETIC POWER FLOW;
1) Charge, 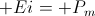 (9)
(9)
2) Discharge, 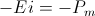 (9)
(9)
DIELECTRIC POWER FLOW;
3) Charge, 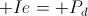 (10)
(10)
4) Discharge, 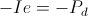 (10)
(10)
The versor expressions for charge and discharge are given as.
(11)
,
,
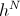 is the charge/discharge versor operator. Substituting these expressions into the general relations of Power Flow, the magnetic,(12)
is the charge/discharge versor operator. Substituting these expressions into the general relations of Power Flow, the magnetic,(12)
,
,
And, the dielectric,
(13)
,
,
Hence the most general expression for Versor Power is,
(14)
, Versor Watts
, Versor Watts
This stored energy can exist in one of two distinct forms,
The Magnetic Energy,
(1) 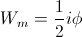 , Ampere-Weber
, Ampere-Weber
The Dielectric Energy,
(2) 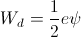 , Volt-Coulomb
, Volt-Coulomb
Because these stored energies are static quantities, they are time invariant. The dimension of time has no role in their existence. It is however that time is a necessary dimensional requirement for the existence of energy. So where then is the energy?
These dimensional expressions for stored energy represent only the Potential for Energy Existence. It is that the expressions given for the energy stored by a field of induction are no more than expressions for the magnitude, and quantity, of the magnetic induction, and dielectric induction, themselves. No union of the two inductions exist to form the product, Electrification, Q, and its time rate, Energy, W.
The single energy transient is a Magnetic Energy Transient, a transient of Electro-Motive Force, E, or it is a Dielectric Energy Transient, a transient of Displacement Current, I. These two reactive transients give rise to products, these with their respective potentials, the electro-static potential, e, and the magneto-motive force, i. M.M.F. is also considered a potential in that it is static. These products of reaction and potential represent The Electrical Activity of their respective Single Energy Transients. Thus a pair of Products, one for each field,
The Magnetic Activity
(3) 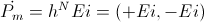 , Watt
, Watt
The Dielectric Activity
(4) 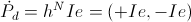 , Watt.
, Watt.
Each Versor Activity, 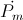 or
or 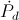 , represents one form of energy only, magnetic or dielectric, not both.
, represents one form of energy only, magnetic or dielectric, not both.
Also shown in part one was the magnification factor is a negative numeric. This magnification factor, n, is the ratio of two time spans, the time span for charge, to the time span for discharge. For the numeric ratio to be negative, one time span must also be negative. Hence the magnification factor is the ratio of a negative time span, the charge time, to a positive time span, the discharge time. The magnification factor is given as
(5) 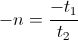 , Numeric
, Numeric
By the Law of Energy Conservation for the stored inductive energy, the amount of energy given to the field must equal the amount of energy that the field can give back. This is to say the energy sent into a field of induction is the same energy sent out of the field of induction. Hence the two energies are in opposition with regard to the flow of power, the power in, and the power out, this resulting in a negative transfer constant, the magnification factor, n.
This results in the expressions for power flow containing a negative dimension, now exists one power flow forward in time, and another power flow, reverse in time. Power can now flow in both directions with regard to the dimension of time. Hence Power is free to move about in the dimension of Time, that is, it is a Versor Power Flow.
Here exists an analog of power flow in space along the length of a transmission line, where power is free to move along the length of the line in either direction. Thus the analog of a “Length of Time”. Here then the existence of forward and reflected waves in time, just as was seen for waves on a transmission line. Hereby a composite transient, the superposition of a wave moving forward in time and a wave moving backward in time, can be developed for any instant in time. One wave travels from the past to the future, the other wave travels from the future to the past, a pair of traveling waves in time, traveling in opposite directions. The superposition of the opposing waves is the Present, or Now, t equals zero.
The versor of Electrical Activity hence resides in the metrical dimension of Time, giving the relation as
(6)  , Seconds.
, Seconds.
Time is now a bi-valent dimension, two values of time,
+ t , real time, seconds,
– t , imaginary time, seconds.
It is then given by the Law of Energy Conservation,
(7) 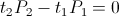 , Watt-Second
, Watt-Second
Imaginary Time can be called “Counter – Time”, this in analog to “Counter – Space”. There is however an important difference between the two. The expression for Counter-Space is given by
(8) 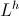 , Per Centimeter
, Per Centimeter
Where h = -1
However, the expression for Counter-Time is given by
(9) 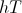 , Negative Second
, Negative Second
Space is given here in terms of algebraic products, whereas Time is given here in terms of algebraic sums. This suggests a relation between Time and Space, or Time – Space where it is
(10)  , Versor
, Versor
(10a) 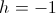 , Unit Versor
, Unit Versor
A similar condition can be found for the versor condition
(11)  , Versor
, Versor
Reducing this to a base two versor,  , gives the pair of projections,
, gives the pair of projections,
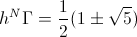 , Numeric
, Numeric
This resulting in a pair of ratios
(13) 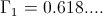 , Numeric
, Numeric
(14) 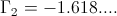 , Numeric.
, Numeric.
Little theoretical knowledge exists on this subject. It is of interest to note here the relations,
(15) 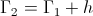 , Numeric
, Numeric
And
(16) 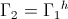 , Numeric
, Numeric
Thus
(17)  , Numeric
, Numeric
In part one the unique condition of a disruptive discharge was given. In the disruptive discharge of a magnetic field of induction, or a dielectric field of induction, the discharged energy is confined within the metallic-dielectric geometry. No external energy transfer exists. In this condition the given field, the magnetic, or the dielectric, exchanges its energy with its Conjugate Form, the dielectric, or the magnetic. This is to say that Every Condenser has a bit of Inductance, it is the very nature of an aether filled metallic-dielectric geometry.
Because this “parasitic” capacitance or inductance has a very small value as a coefficient of energy storage, the Disruptive Discharge Develops Transients of great intensity and of Very Short Duration in Time. For the discharging inductor the intensity is given by
(18) 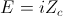 , Volts
, Volts
Where
(19) 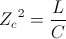 , Henry Per Farad
, Henry Per Farad
And C is the Parasitic Capacitance
And for the Discharging Condenser,
(20) 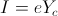 , Ampere
, Ampere
Where
(21) 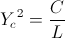 , Farad per Henry
, Farad per Henry
And L is the Parasitic Inductance.
Because one form of energy storage is the denial of the other form of energy storage, in the disruptive discharge, no steady state condition is possible. The energy has nowhere to roost, it is continuously thrown back and forth, remaining within the metallic-dielectric geometry. Here the stored energy is continuously exchanged between spatial and counter-spatial forms of energy storage, this continuously moving back and forth thru time and counter time. Because the Inductance in the steady state is a short circuit, it cannot maintain a potential, e, and because the Capacitance in the steady state is an open circuit, it cannot maintain a current, i. Thus a potential, e, can only exist as a time variant E.M.F., E, and likewise a current, i, can only exist as a time variant displacement, I.
No energy is transferred into, or out of, the metallic-dielectric geometry, it is only exchanged between denials of form. It is then given
(22) Ei = -Ie , Volt-Ampere
-Ei = Ie , Volt-Ampere
Substituting the following
(23) E = e , Volt
I = i , Ampere
Gives the expression for the electrical activity of the disruptive discharge as
(24) 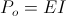 , Volt-Ampere
, Volt-Ampere
Instead of allowing the disrupted Field of Induction to discharge back into its conjugate form within the metallic-dielectric geometry, an external conjugate form can be utilized. That is to say, an External Condenser, or an External Inductor. Equations (19) and (21) now apply to the external energy storage element rather that the internal parasitic values. These represent the natural impedance of the pair of energy storages. The metallic-dielectric geometry now is reduced to a magnetic inductance connected with an external condenser, or it is reduced to a dielectric capacitance connected with an external inductor. This is given in a sequence of diagrams, Fig 1.
(1) Fig 1A. A discharging Magnetic Inductance transfers its energy into a Charging Dielectric Capacitance.
(2) Fig 1B, A discharging Dielectric Capacitance transfers its energy into a Charging Magnetic Inductance.
(3) Fig 1C, A charging Magnetic Inductance transfers its energy out of the Discharging Dielectric Capacitance.
(4) Fig 1D, A charging Dielectric Capacitance transfers its energy out of the Discharging Magnetic Inductance.
Here given are the four quadrants of energy exchange between a pair of mutually conjugate forms of energy storage, the inductor and the condenser. The stored energy is being continuously transformed from one form into its conjugate form in an endless cyclic rate. The time rate of this energy exchange is the electric activity, 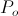 , in volt-amperes. This activity represents the flow of power between the Inductor and the Condenser. Rather than a single energy transfer, it is now a pair of energy transfers. This is now a double energy transfer, or a Double Energy Transient.
, in volt-amperes. This activity represents the flow of power between the Inductor and the Condenser. Rather than a single energy transfer, it is now a pair of energy transfers. This is now a double energy transfer, or a Double Energy Transient.
In the double energy transient the stored energy is trapped with no escape. Thus this energy remains stored energy in an alternating current form, stored A.C. energy. The activity, or the flow of power is a continuous cyclic energy exchange, an opposing pair of energy transfers each moving in opposite directions in time. One energy transfer travels forward in time, the conjugate energy travels backward in time. The superposition of this opposing pair of traveling waves in time gives rise to a stationary wave in time. This is an analog to the standing wave on the length of a transmission line.
Because the inductor is charging while the condenser is discharging, or the condenser is charging while the inductor is discharging, the relations for power flow are given by
(25) 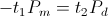 , watt-second
, watt-second
And rearranging gives the relation
(26) 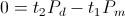 , watt-second
, watt-second
The expression of the Law of Energy Conservation.
For the condition of oscillatory energy exchange the time relations are given by
(27)  , seconds
, seconds
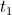 , and the discharge time span,
, and the discharge time span, 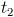 , are now equal and opposite. Hence a single time span can represent both
, are now equal and opposite. Hence a single time span can represent both 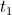 and
and 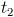 .
.
(28) 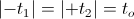 , seconds.
, seconds.
This time span is the one quarter period of a complete cycle of Energy Exchange, T. In the condition of cyclic energy exchange the magnification factor is expressed by the relation
(29) 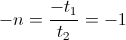 , versor.
, versor.
Hence the magnification factor is always unity. The Magnetic Power, Pm, is equal to the Dielectric Power, Pd. This is to say the Charge Power Flow is equal to the Discharge Power Flow. No charge-discharge magnification exists here. This magnification factor is now just a versor operator establishing the Law of Energy Conservation.
For the condition of energy transfer, the single energy transient, the transfer of energy is into, or out of the single stored energy. It is a one way flow, backward flow, or forward flow. It is uni-directional like a direct current. However, for the condition of the double energy transient the energy is reflected back upon itself between an opposing pair of energy storages. The double energy transient is a bi-directional power flow like an alternating current.
The single energy transient can be considered a traveling wave in time, the double energy transient can be considered a standing wave in time. This is in analogy to traveling and standing waves on a transmission line. Here time is an analog of length in the movement of electric energy.
The activity of the oscillatory energy exchange is given by the product of the Electro-Motive Force, E, and the Displacement Current, I. The four quadrantal activities are thus given by,
Fig, 1A, -EI
Fig, 1B, -IE
Fig, 1C, +EI
Fig, 1D, +IE
Each of the above activities exist in their respective quadrant in the cycle of energy exchange. It is given algebraically that,
(30) -EI = -IE
+EI = +IE
No energy is gained or lost, thus the activity is identical for each quadrant in the time cycle of energy exchange. Hereby a single effective activity exists for the double energy transient in its exchange of energy between Magnetic Form and Dielectric Form. This is given as in equation (24)
(24a) Po = EI volt-ampere
This is the electric activity of the oscillatory energy exchange between the Inductor and the Condenser. This is not an actual power in watts, but an electric activity in volt-amperes.
For the condition of energy transfer, the single energy transient, a pair of electrical activities exist,
eI , iE , watts.
Each represents the flow of power in the Dielectric, or Magnetic Energy Transfer. Here the charge time span and the discharge time span are independent time frames. An indefinite static time interval can exist between these two time frames. However, the double energy transient of oscillatory energy exchange has no possible static time interval, no possible steady state. Also the charge time span is identical to the discharge time span. One is the mirror image of the other, both of equal length in time. The two opposing energy transfers cancel out, just as do two opposing traveling waves. This leads to a stationary wave and one resultant electric activity only, that of the Cyclic Energy Exchange. No energy is gained or lost, it is confined to the oscillating system. This represents a stored alternating current and as such must posses an angular velocity of energy exchange since A.C. is a circular function. Hence it is,
(31) 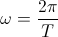 , radian per second
, radian per second
Where T is the time span of one cycle of energy exchange.
This exchange is then in the form of a perpetual motion which gradually weakens due to energy leakage, that is, the losses in the metallic-dielectric geometries where the energy exchange takes place.
Power magnification in the oscillating energy transfer takes on a different form in the oscillating energy exchange. No magnification is possible between the charge and discharge portions of the cycle of energy exchange, they are equal and opposite time spans. It is however that a finite quantity of stored energy exists, and its activity is the time rate of energy exchange between magnetic and dielectric forms. A definite time cycle exists, where the transfer time, to, is one fourth the time span of a complete cycle of energy exchange, T. The transfer time defines the rate at which the stored energy is transferred back and forth, that is, the rate at which it is exchanged. Thus the relations for power and energy are given by
(32) 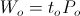 watt-second
watt-second
(33) 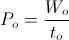 watt, or volt-ampere.
watt, or volt-ampere.
Where to is one fourth period T. The Time Period, T, and thus the angular velocity of energy exchange can be derived from the Laws of Induction, these for an alternating current form. Thus given
The Law of Magnetic Induction,
(34) 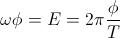 , weber per second
, weber per second
(38) 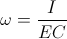 , and
, and 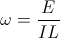 , radians per second
, radians per second
It is however,
(39)  , and
, and 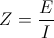 siemens, ohm
siemens, ohm
Thus the relations (38) become,
(40) 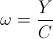 , and
, and 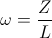 , radians per second
, radians per second
Substituting the defining ratios,
(41) 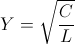 , and
, and 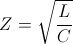 , siemens – ohm
, siemens – ohm
Into relations (40) gives the expressions for the angular velocity of energy exchange
(42)  , and
, and  , radian per second
, radian per second
Hence (42a) 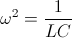 , by definition.
, by definition.
The expressions (42) for the angular velocity of energy exchange represent a pair of velocities, one forward in time, one reverse in time. The time period of one cycle of energy exchange is therefore given by the expression,
(43) 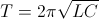 , seconds
, seconds
And thus the time span of energy transfer is given by
(44) 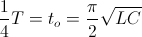 , seconds
, seconds
Substituting these relations into the expression for power, equation (33), where it is,
(43a) 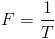 , per second
, per second
The Law of Dielectric Induction,
(35) 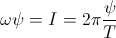 , coulomb per second
, coulomb per second
Rearranging (34) and (35) gives
(36) 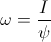 , and
, and 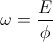 , radians per second
, radians per second
And substituting the relations
(37) 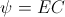 , and
, and  , Induction
, Induction
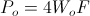 , volt – amperes
, volt – amperes
Where, F, is the frequency of oscillation, in cycles (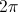 radian) per second. Hence the magnification of activity for a given quantity of energy in the oscillating energy exchange is not a function of the ratio of charge to discharge times, since they are now equal. The magnification is here given as a function of the rate of energy exchange, the Frequency of Oscillation, F, in cycles per second. The more rapid the energy exchange, the higher the frequency and thus the larger the magnitude of the resulting electric activity. Power is directly proportional to frequency.
radian) per second. Hence the magnification of activity for a given quantity of energy in the oscillating energy exchange is not a function of the ratio of charge to discharge times, since they are now equal. The magnification is here given as a function of the rate of energy exchange, the Frequency of Oscillation, F, in cycles per second. The more rapid the energy exchange, the higher the frequency and thus the larger the magnitude of the resulting electric activity. Power is directly proportional to frequency.
In the above condition of energy exchange the charge time span is equal in length to the discharge time span. No charge/discharge magnification is possible. It is however that the energy storage coefficients, the Inductance L, and the Capacitance, C, can be altered between charge and discharge intervals, Fig 3. This alteration can be done in two ways. One method is to use separate inductive elements in the charge/discharge cycle. For example, an inductance can take energy from one capacitance on charge and deliver this energy to another capacitance on discharge, or alternately a capacitance can take energy from one inductance on charge and deliver this energy to another inductance on discharge. Energy exchange has now reverted to a pair of energy transfers, and an indefinite static interval. The frequency of oscillation is according different for the different charge or discharge intervals. Hence the magnification factor is given by the relation
(46) 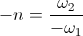 , numeric
, numeric
Where 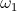 is the angular time rate of charge and
is the angular time rate of charge and  is the angular time rate of discharge. This magnification was utilized by Nikola Tesla for the purpose of Power Amplification with no electronic elements.
is the angular time rate of discharge. This magnification was utilized by Nikola Tesla for the purpose of Power Amplification with no electronic elements.
The other method of altering the charge/discharge cycles is thru synchronous Parameter Variation. Rather than switching the energy storage elements, the co-efficients of energy storage, L, and, C, can be made variable throughout the cycle of Alternating Energy Exchange. Hereby the capacitance can vary between charge and discharge intervals, or the inductance can vary between charge and discharge intervals, and both can be varied throughout the cycle of alternating energy exchange. The magnification factor is now a complex quantity, or versor expression. Little theoretical knowledge exists on this subject.
The relations for electric activity for differing charge and discharge frequencies are hereby the same expressions as those for single energy transfer,
(47) 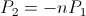 , volt-ampere
, volt-ampere
(48) 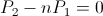 , volt-ampere
, volt-ampere
(49) 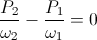 , volt-ampere-second
, volt-ampere-second
Equation (49) states the Law of Energy Conservation, this for the condition of switching energy storage elements. Since the magnification factor is a complex quantity for the condition of Synchronous Parameter Variation, the Law of Energy Conservation is indeterminate.
In all that has been covered thus far the Metrical Dimension of Time has been the primary consideration. Energy and Power are Products of Time. This is expressed in the relation
(50) 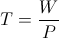 , joule per watt
, joule per watt
The relationship between Energy and Power is Time. The energy has been a stored energy, and the power has been the time rate of the stored energy movement.
What has not been considered thus far is the condition of an actual Direct Current, a Time Invariant Condition, nor the condition of negligible co-efficients of energy storage, very insignificant values of inductance or capacitance. These are conditions of Zero Energy Storage. The dimension of time has no role in these conditions. This is the “Time Scalar” condition. Here is the fourth and final condition in the Flow of Electric Power.
In the scalar condition the transfer of energy exists with no form of energy storage, there is no charge or discharge interval. The transfer is constant. As it was in the beginning, so it shall be for now and ever more, the continuous, or Direct Current. Even with the application of an alternating current, the energy transfer is still direct, it following exactly the cycle of the applied alternating current. Hence the scalar condition is FREQUENCY INDEPENDENT, as would be expected for a time invariant condition. Thus the transfer can be instantaneous. Time does not exist in the scalar condition. The notions of constant, cyclic, or instantaneous, play no part in this condition. They can only arise from external causes.
The scalar condition is then the result of one of two distinct conditions,
1) No time variation of the fields of induction, as with direct current,
2) Negligible energy storage so as not to react with time variant currents, as with transient current.
In both conditions the Electro-Motive Force, E, and the Displacement Current, I, are zero. Hence no energy exchange or transfer exists with any field of induction.
Because the dimension of time in the scalar condition is indeterminate the dimensional relation of energy is also indeterminate, since energy is a product of time. It is however that power flow actually takes place as a product of the potential, eo, and the current, io, that is,
(51)  , watt
, watt
It is however
(52) 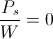 , per second
, per second
This is to say that the time span is indefinite. Hence energy can only be expressed as power in the time scalar condition.
Also, in the absence of an electric field of induction both phi and psi are non-existant, thus the product, Q, is non-existant,
(53) 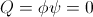 , planck.
, planck.
Therefore the energy is non existent
(54) 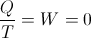 , joule
, joule
So where then is the energy? In the scalar condition all energy is created and dissipated in the same instant, no intermediary energy exists. It is “on demand”. Obviously, as with the similar situation of the disruptive discharge condition, there is always a bit of something somewhere that leads to a determinate solution, such as the connecting wires. The actual scalar condition can only exist within inter-molecular dimensions.
The scalar condition can be derived by the interconnection of resistances and conductances. Resistance, R, in Ohms, and Conductance, G, in Siemens. No energy storage is possible in these elements and thus they are Time Invariant quantities. There is no energy, what ever energy is given here instantly vanishes, appearing as a source of heat. This scalar condition thus contains no electricity, it simply eliminates it. The rate at which energy is eliminated is given as a flow of power, P, in watts, this as a product of a dissipative E.M.F. and a dissipative displacement.
-e, , E.M.F.
-i , Displacement
Because of the scalar condition it is the E.M.F. is also the Potential, and the displacement also the current. No electric field exists. Thus the power is given by
(55) 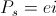 , watt.
, watt.
In a manner similar to the condition for oscillating energy exchange, no cross product exists between a reaction and a potential, as it is with the relation
(24) 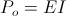 , volt-ampere
, volt-ampere
(56) 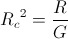 , ohm per siemens
, ohm per siemens
(57) 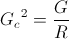 , siemens per ohm
, siemens per ohm
And
(58) 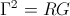 , scalar numeric.
, scalar numeric.
Where
Rc , the natural resistance
Gc , the natural conductance
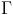 , the propagation constant.
, the propagation constant.
The scalar condition can also exist for the interconnection of receptances and acceptances, receptance, H, in Ohm, and Acceptance, S, in Siemens. Here the energy is instantly produced, drawn out of the inter-molecular dimensions of the receptances and acceptances. With the resistance-conductance configuration the energy is instantly destroyed, pulled into the intermolecular dimensions of the resistances and conductances. Both are instant, no lag time is involved.
These conditions can be established with a pair of unit drycells. This condition involves time invariant energy transfer. It is instantaneous. When a charged unit drycell is connected with a discharged unit drycell a constant unidirectional transfer of energy takes place. This transfer is in space, not in time. This transfer takes place from the charged drycell to the discharge drycell, a one way trip.
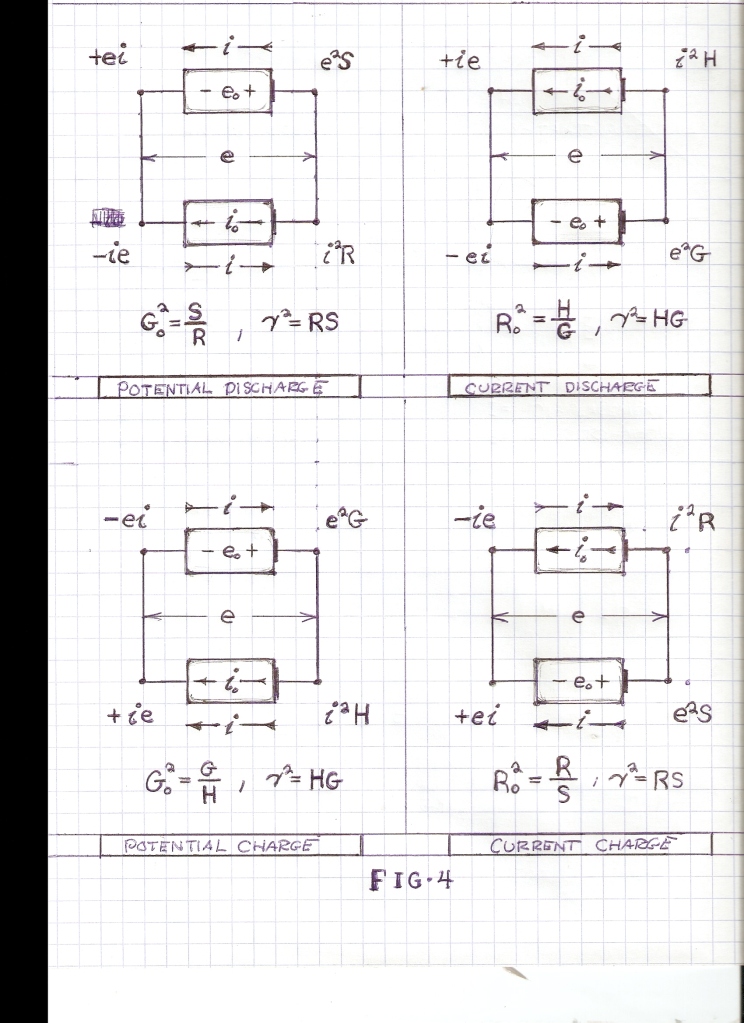
As with the prior conditions of energy movement four relations exist with regard to the flow of power. These are shown in the diagrams of Fig 4. Hence the four relations,
Fig, 4A, -ei , watts
Fig, 4B, -ie , watts
Fig, 4C, +ei , watts
Fig, 4D, +ie , watts
And algebraically it is given
(58) -ei = -ie , watts
+ei = +ie , watts
The transfer of energy and thus the flow of power is bi-directional, any drycell can charge any other drycell, that is,
-ei & +ei.
And hereby the flow of power is given as
(59)  , watts
, watts
In the scalar condition there is no electrical activity because of the time invariant nature of this condition. Likewise, in the exchange condition there is no electrical power because of the time variant nature of this condition. One is NOT the other. Thus the relations are,
(60) 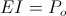 , volt-amperes,
, volt-amperes,
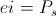 , watts.
, watts.
Both are real quantities and thus algebraically additive. The volt-amperes represents the complete storage of energy with no leakage whereas the watts represents the complete absence of energy storage with the complete leakage of energy. Here “leakage” is defined as leakage into, or out of, the metallic-dielectric geometry.
Here in final form are thus the four distinct conditions for the flow of power in an electrical configuration:
0) The Scalar, or Anti-Electric, Product;
(61)  , watt
, watt
1) The Forward Cross, or Magnetic, Product;
(62) 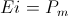 , joule per second
, joule per second
2) The Axial, or Magneto-Dielectric, Product
(63) 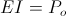 , volt-ampere
, volt-ampere
3) The Reverse Cross, or Dielectric, Product
(64) 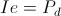 , joule per second
, joule per second
Hereby the Heaviside Expression for the Movement of Energy as a flow of power can be assembled, giving the general form as,
(65) 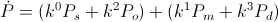
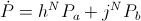 , versor watt
, versor watt
The apparent power flow is given as the square root of the sum of the squares,
(66) 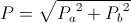 , watt
, watt
Where 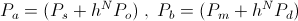 , watt
, watt
(67) 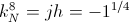 , versor
, versor
(67a) 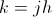 , versor
, versor
The Three Fundamental Factors can now be derived for the electrical configuration, utilizing equations (65) and (67), hence given are,
(68a) 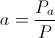 , Power Factor, percent
, Power Factor, percent
(68b) 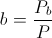 , Induction Factor, percent
, Induction Factor, percent
(68c) 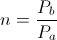 , Magnification Factor, numeric
, Magnification Factor, numeric
Where it is,
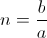 , numeric
, numeric
For the condition of equation (66) it is a circular function and
(69)  , unity
, unity
And the general versor expression is given as,
(70)  , versor
, versor
Taking equation (66) as
(66a) 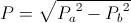 , watt
, watt
As the condition of a hyperbolic function fives the relation
(71) 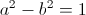 , unity
, unity
And the general versor expression is given as
(72) 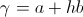 , versor
, versor
It can be seen that each quadrant is in itself another four quadrant relation. One relation is compounded with another. The versors are inordinately complex, back to the J. S. Bach. These relations given are found in “The POWER of Music, Alexander’s Feast”, by G.F. Handel, The Final Choral Movement. Consider this required listening.
73 DE N6KPH SK.